선형 변환

선형 변환(linear transformation)은 선형성(덧셈성질과 균일성)을 만족하는 두 벡터 공간 사이의 함수이다. 수학적 정의는 다음과 같다.

실수계(real number field)에 속해있는 두 벡터 공간 V와 W를 가정하자. 이 때 벡터 공간 V에 속해있는 두 벡터 x, y와 실수 스칼라 a에 대해 다음의 법칙이 성립되는 함수 f : V → W는 선형 변환이다.

$f(x+y)=f(x)+f(y) \,$	덧셈성질, 중첩의 원리(additivity)
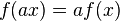$f(ax)=af(x) \,$	균질성, 균일성(homogeneity)

이 때, 기준이 되는 계는 꼭 실수계일 필요는 없으며 다른 어떤 계에 대해서도 성립할 수 있다.

위의 정의를 확장하면 다음과 같이 나타낼 수 있다.

모든 선형 변환은 벡터 x₁, ..., x_m와 스칼라 a₁, ..., a_m에 대해

$f(a_1 x_1+\cdots+a_m x_m)=a_1 f(x_1)+\cdots+a_m f(x_m)$ 의 공식을 만족한다.

선형 변환의 한 예로 n 차원 열벡터 x, m차원 열벡터 b, m × n 행렬 A에 대해 Ax=b의 연산을 하는 경우를 생각해 볼 수 있다. 이 때 행렬 A는 선형 변환을 정의한다.

선형 변환은 앞의 예와 같이 벡터와 행렬의 곱의 연산으로 표현하는 경우가 많다.

다음은 행렬로 표현한 여러가지 2차원 선형 변환의 예이다.

Jang Won Hee