행렬
위키백과 ― 우리 모두의 백과사전.
행렬(行列, matrix)은 수를 네모꼴로 배열한 것으로, 늘어놓은 수들을 괄호로 묶어 표현한다.
목차[숨기기] |
[편집] 정의
행렬의 가로줄을 한자어로 행이라고 하고, 세로줄을 열이라고 한다. 여기에서 행렬이라는 이름이 유래했다.
- 예)

위의 예에서 행렬 A는 두 개의 행 세 개의 열로 이루어져 있다. 어떤 행렬이 m개의 행과 n개의 열로 구성되어 있으면, m by n 행렬, 또는 m×n 행렬이라고 쓴다. m과 n은 차원(次元, dimension)이라고 한다.
aij는 A행렬의 i번째 행, j번째 열에 있는 원소를 뜻한다.
벡터를 1행 행렬 또는 1열 행렬로 생각할 수도 있다. 수를 1x1 행렬로 생각할 수도 있다.
[편집] 연산
[편집] 덧셈
행렬의 합은 같은 자리에 있는 원소의 합으로 정의한다.
- (A + B)ij = Aij + Bij
- 예)

- 예)
[편집] 스칼라 곱
한 행렬에 숫자를 곱하는 연산은, 각 원소에 그 수를 곱하는 방식으로 정의한다.
- (kA)ij = kAij
- 예)

- 예)
[편집] 곱셈
행렬 간의 곱은 다음과 같이 정의한다.
(AB)ij = ∑ AikBkj k
이 때, A의 열 개수와 B의 행 개수가 같아야 곱셈이 정의된다.
- 예)

또한, 행렬의 곱은 비가환 곱이다. AB와 BA가 모두 정의된다고 해도, 이 두 결과는 같지 않을 수 있다.
[편집] 정사각행렬
정사각행렬(Square Matrix)은 행의 수와 열의 수가 같은 행렬을 말한다.
예를 들어 2x2, 3x3, 4x4 행렬 등이다.
[편집] 행렬식
- 이 부분의 본문은 행렬식입니다.
행렬식(determinant)은 det(A) 또는 A 로 표시하며 선형 행렬 A의 크기를 나타낸다. 행렬 2x2 행렬 A가
와 같이 주어진다면, det(A)는
- det(A) = ad − bc
와 같이 정의된다.
[편집] 특수한 행렬
영행렬이란 행렬의 모든 원소의 값이 0인 행렬을 말한다. 영행렬은 덧셈에 대한 항등원이다.
단위행렬은 정사각행렬 중에서 행 번호와 열 번호가 같은 위치의 값은 1이고, 나머지는 0을 가지는 행렬을 말한다. 이 행렬은 곱셈에 대한 항등원이다.
역행렬이란 어떤 행렬의 곱셈에 대한 역원이다.


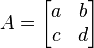


댓글 없음:
댓글 쓰기